Valor Presente Neto (VPN)

Valor Tiempo del Dinero

El concepto del Valor Tiempo del Dinero se sitúa en el corazón de la teoría financiera, reflejando una verdad elemental: un monto de dinero poseído hoy tiene un valor intrínsecamente mayor que el mismo monto recibido en el futuro. Esta premisa, esencial para cualquier análisis de valoración financiera, se apoya en la percepción de que, inherentemente, el dinero en el presente es más valioso que el dinero en el futuro. La esencia de esta diferencia radica en la Tasa de Interés, que puede ser entendida como el pago porcentual otorgado a quien presta dinero por un periodo específico. Esta tasa, generalmente positiva, indica que el prestamista recuperará una cantidad mayor a la originalmente prestada, subrayando la importancia del momento en que se dispone del dinero.

La positividad de la tasa de interés se explica desde varias perspectivas. Primero, desde una visión conductual, la mayoría de las personas muestran una preferencia clara por el consumo inmediato frente al futuro. Esta inclinación natural hacia el disfrute presente sobre el aplazado, sugiere que en ausencia de una recompensa (interés), la disposición a prestar sería significativamente menor. Además, el fenómeno de la inflación, donde el valor de compra del dinero disminuye con el tiempo debido al incremento en los precios de bienes, también juega un papel crucial. Aquí, la tasa de interés no solo debe compensar la preferencia por el consumo inmediato, sino también el incremento en el costo de vida, asegurando así que el prestamista pueda disfrutar de una mayor capacidad de compra en el futuro.

Otra dimensión importante es la demanda de dinero. Por ejemplo, si alguien descubre petróleo en su propiedad y necesita capital para explotarlo, se enfrenta a una decisión crítica: pedir dinero prestado, asumiendo una tasa de interés, o perder la oportunidad. En este caso, la decisión de endeudarse es sensata si los retornos del proyecto superan el costo del préstamo.

En resumen, la tasa de interés y, por ende, el Valor Tiempo del Dinero, se ajustan de acuerdo a la oferta y demanda de capital. Si hay escasez de dinero (alta demanda), las tasas tienden a incrementarse, incentivando el préstamo. Por el contrario, una abundancia de capital (baja demanda) puede llevar a una reducción en las tasas. Este concepto es un pilar fundamental en las finanzas, afectando desde decisiones personales hasta estrategias corporativas a gran escala, y subraya la importancia de considerar el momento exacto en el que se dispone del dinero en cualquier evaluación financiera.

Valor Presente (o Valor Actual) en relación con los flujos de caja

Los flujos de caja son cantidades de dinero que se reciben o pagan en diferentes momentos, considerándose positivos si se reciben y negativos si se pagan.

La tasa de interés de equilibrio en el mercado de capitales es la que iguala la oferta y demanda de dinero, y es comúnmente expresada en términos anuales. Por ejemplo, si se presta $100 a una tasa del 10% anual, al final del año se recibirá $110. Esto también implica que se puede pedir prestado dinero con la promesa de devolver una cantidad mayor en el futuro debido al interés.

El Valor Presente (VP) de una cantidad futura considera el dinero hoy como «equivalente» a una cantidad mayor en el futuro, ajustada por la tasa de interés. Por ejemplo, $100 hoy es equivalente a $110 en un año si la tasa de interés es del 10%. Esto se debe a que se puede modificar la fecha de un flujo de caja, adelantándola o posponiéndola, lo que altera su valor debido al tiempo y al interés.

La fórmula para calcular el Valor Presente de un flujo de caja futuro es:

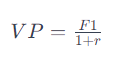
donde F1 es el flujo de caja en el próximo año, r es la tasa de interés anual, y VP es el valor presente. En el ejemplo dado, F1 es $110, r es 0.10 o 10%, y el VP es $100. Esta fórmula ayuda a determinar el valor actual de una cantidad futura, tomando en cuenta el costo de oportunidad del dinero.

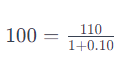
¿Qué pasa si el préstamo se hace a un período mayor a un año?

Si un préstamo de $100 se hace a una tasa de interés del 10% anual por un período de dos años, al final del primer año la deuda sería de $110. Este monto se vuelve a invertir al mismo interés del 10% para el segundo año, lo que lleva a una deuda final de $121. Para calcular el valor presente de este monto ($121) que se pagará en el segundo año, es necesario descontar la tasa de interés dos veces, ya que el dinero en el futuro es menos valioso que el dinero en el presente debido al tiempo y la oportunidad de ganar interés.

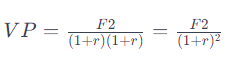
Donde:

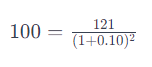
Ejemplo Valor Presente

Imaginemos que queremos recibir $600 en 5 años. ¿Cuánto necesitamos invertir hoy si la tasa de interés es del 8% anual? Aquí es donde la fórmula del VP se convierte en nuestra herramienta esencial.

La fórmula para calcular el VP es la siguiente:

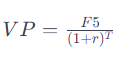
Donde:

Al aplicar estos valores a la fórmula, obtenemos:

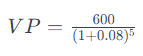
Al realizar el cálculo, encontramos que el Valor Presente de una inversión que nos pagará $600 en 5 años, con una tasa de interés del 8%, es aproximadamente $408.35. Esto significa que si invertimos $408.35 hoy en una cuenta o instrumento que nos ofrezca un 8% de interés anual, tendríamos $600 después de 5 años.

Valor Presente Neto (VPN o VAN)

Hasta el momento hemos hablado del valor presente, ese pilar fundamental que nos permite entender el valor actual de los flujos de caja futuros. Pero, ¿cómo integramos el costo inicial de una inversión en esta ecuación? Ahí es donde entra en juego el Valor Presente Neto (VPN) o Valor Actual Neto (VAN), una extensión del valor presente que considera tanto los ingresos futuros como los desembolsos iniciales.

El VPN o VAN es una herramienta de análisis financiero que nos ayuda a tomar decisiones informadas. Se calcula restando la inversión inicial del valor presente de los flujos de caja futuros. En otras palabras, no solo consideramos lo que vamos a recibir, sino también lo que ya hemos pagado. Esta visión integral nos permite evaluar si un proyecto o inversión vale la pena financieramente.

La fórmula que utilizamos para calcular el VPN/VAN es:

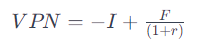
Donde I representa la inversión inicial, F es el flujo de caja que se espera recibir en el futuro, y r es la tasa de interés o el costo de capital. La belleza de esta fórmula radica en su simplicidad y poder predictivo. Nos indica claramente si el valor actual de los beneficios futuros supera el costo de nuestra inversión inicial.

Ejemplo Valor Presente Neto

Con una inversión inicial de $100 y un flujo de caja de $110 recibido al final del primer año con una tasa de interés del 10%, la fórmula para el VPN es:

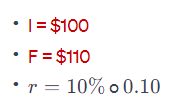
La fórmula se calcularía como:

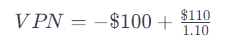
Primero calculamos el valor presente del flujo de caja de $110, dividiéndolo por 1.10, que da $100. Ahora, restamos la inversión inicial de $100.

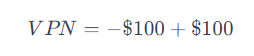
El VPN resultaría en:

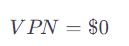
Esto indica que el valor presente neto de recibir $110 en un año después de invertir $100 hoy, con una tasa de interés del 10%, es de $0, lo que significa que la inversión cubre exactamente el costo de oportunidad del 10% sin generar ganancia adicional.

• Que pasaria la tasa de interes es de 15%

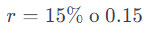
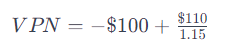
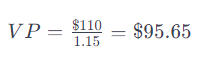
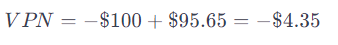
Con una tasa de interés del 15%, el VPN de recibir $110 en un año después de invertir $100 hoy es de aproximadamente -$4.35, lo que sugiere que la inversión no cubriría el costo de oportunidad del 15%, resultando en una pérdida.

• Que pasaria la tasa de interes es de 5%

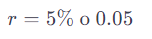
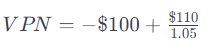
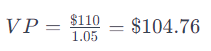
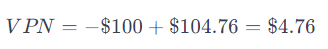
Con una tasa de interés del 5%, el VPN de recibir $110 en un año después de hacer una inversión inicial de $100 hoy es aproximadamente $4.76, lo que indica que la inversión generaría una ganancia por encima del costo de oportunidad del 5%

En resumen:

Ejemplo 2 VPN

Imaginemos que la empresa «Dulces Horneados S.A.» está considerando la compra de un nuevo horno para expandir su producción. La inversión inicial para el horno es de $10,000. Se estima que el horno incrementará los flujos de caja anuales de la empresa debido a una mayor capacidad de producción y eficiencia energética. Después de un análisis del mercado y las proyecciones de ventas, la empresa calcula que el horno generará flujos de caja adicionales de $2,000 al año durante 7 años. La empresa utiliza una tasa de descuento del 8% para evaluar sus inversiones.

Para calcular el Valor Presente Neto (VPN) de la inversión en el horno, usaríamos la siguiente fórmula:

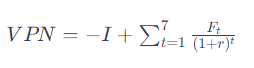
Donde:

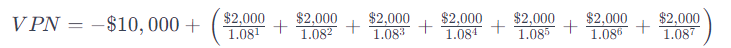
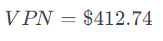
Este resultado positivo de VPN indica que la inversión es financieramente rentable. En términos prácticos, significa que «Dulces Horneados S.A.» no solo recuperaría los $10,000 invertidos inicialmente en el horno, sino que también obtendría un beneficio adicional de $412.74 por encima del costo de oportunidad del 8%. Esto hace que la compra del horno sea una decisión acertada desde el punto de vista financiero y sugiere que la empresa puede esperar un retorno satisfactorio de su inversión, justificando así la expansión de su capacidad de producción.